Оценка скорости алгоритмов¶
Как оценить скорость работы алгоритма¶
- Если необходимо сделать оценку скорости, то нужно делать замеры для большого количества значений (размера входных данных). Чем больше точек - тем точнее данные
- можно брать значения по линейно
- можно брать по логарифмической шкале
- иногда итмеет смысл брать значения чуть ли не непрерывно, потому что в таком случае можно посмотреть на динамику, когда происходит выделение памяти etc
- Также стоит делать замеров, чтобы получать усреденные значения
- Просто замерять время между выполнением команд может быть недостаточно точно - т.к. в процесс мог влезть другой процесс и так далее. Нужно мерять cpu time
Какие есть интрументы для измерения¶
Python
- если вы используете ipython, есть magic %%time и %%timeit
- есть библиотека profile
C++
- функции из chrono :)
- vallgrind's callgrind
- gperftools
Java
- ссылка - список профайлеров
Mergesort¶
Краткое описание¶
- Нужен механизм разделения
- Алгоритм для сортировки минимальной подзадачи
- Алгоритм объединения (merge)
Будем делить массивы ~пополам, учитывая, что один их размер может быть нечетным
Сколько всего будет разбиений?
Сам алгоритм:
1 MergeSort(Array, end): 2 Copy = CopyArray(Array) 3 SplitMerge(Copy, 0, n, Array) 4 5 6 SplitMerge(Copy, begin, end, Array): 7 if end - begin < 2 8 return 9 middle = (end + begin) // 2 10 SplitMerge(Array, begin, middle, Copy) 11 SplitMerge(Array, middle, end, Copy) 12 Merge(Copy, begin, middle, end, Array)
- постоянно меняются местами Array и Copy - данные копируются из одного в другой
Функция Merge - время работы
</font>
Достаем двойные листочки!¶
Давайте напишем Merge (и весь алгоритм), определение MergeSort выглядит довольно простым.
- Идея: есть два массива одинакового рамера, второй разбит на две части
- Переносим элементы в первый массив из второго либо из первой, либо из второй части


[[1, 1, 1, 1], [2, 3, 4, 5]]
[1, 1, 1, 1, 2, 3, 4, 5]
[["2",3,4,5], [1,1,1,"1"]]
[1,1,1,1,2,3,4,5]
Merge¶
1 Merge(Array, begin, middle, end, Copy): 2 fst, snd = begin, middle 3 for ptr in range(begin, end) 4 if fst < middle and (snd >= end or Array[fst] <= Array[snd]) 5 Copy[ptr] = Array[fst] 6 fst += 1 7 else 8 Copy[ptr] = Array[snd] 9 snd += 1
Сложность, плюсы, минусы, стабильность¶
Если посмотреть еще раз на это изображение:

- становится интуитивно понятно, какая у алгоритма сложноcть.
- - на
Mergeна каждом "уровне" - уровней
- получается сортировка </font>
Плюсы сортировки¶
- Гарантированная скорость
- Стабильность
- Возможность параллелизации
- Модификации используются для внешней сортировки
- Подходит хорошо для списков (см. далее) </font>
Минусы¶
- памяти - без оптимизаций
- Немного медленнее Quicksort </font>

</font>
Варианты¶
Как можно усовершенствовать Mergesort (много как, на самом деле)
Сделать параллельным¶
1 SplitMerge(Copy, begin, end, Array): 2 if end - begin < 2 3 return 4 middle = (end + begin) // 2 5 fork SplitMerge(Array, begin, middle, Copy) 6 join 7 SplitMerge(Array, middle, end, Copy) 8 Merge(Copy, begin, middle, end, Array)
Fork-join model¶
Это стандартный подход, исользующийся для алгоритмов "Divide-and-Conquer". На этот каркас можно "натянуть" и другие алгоритмы
1 Solve(problem): 2 if problem is small enough: 3 solve problem directly (sequential algorithm) 4 else: 5 for part in Subdivide(problem) 6 fork subtask to Solve(part) 7 join all subtasks spawned in previous loop 8 return combined results</font>
Другие идеи¶
- Использовать имеющиеся в данных убывающие / возрастающие посоледовательности (и не сортировать их)
- Можно превратить в блочную сортировку
- В модификации хорошо работает со списками - когда доступ по индексу закрыт. При этом можно обойтись без доп. памяти/ </font>
Quicksort¶
Идея¶
- Выбрать стержневой элемент
- Разбить массивы так, чтобы "слева" от стержневого были элементы , "справа" - большие
- Повторять для "правой" и "левой" половин, пока длина массива > 1 </font>
Особенности алгоритма¶
Фичи и плюсы¶
- Алгоритм придумал Хоар для быстрой сортировки словарей (1959)
- Алгоритм обладает средним временем работы , но наихудшим
- При этом у него хорошие константы
- Не нужно дополнительно выделять память
- Можно распараллелить
Недостатки¶
- нестабилен
- не гарантированно быстр (может "тормозить")
- нестабилен </font>
Псевдокод¶
1 Quicksort(Array, begin, end): 2 if begin < end: 3 pivot = Partition(Array, begin, end) 4 Quicksort(Array, begin, pivot) 5 Quicksort(Array, pivot+1, end)</pre> </font>
Процедура Partition¶
Итак, есть сигнатура: Partition(Array, begin, end) -> pivot
Что эта функция должна делать?
И как ее реализовать (как минимум один способ)? </font>
На семинаре демонстрировалось неправильное изображение! Здесь приведен исправленный вариант.
- Использовалось 1-индексирование, сказано про это не было - теперь псевдокод исправлен на 0-индексирование
- Была показана работа
Partitionдля создания убывающих массивов (вместо возрастающих, как в коде) - Если -й элемент меньше либо равен стержневого, то меняются местами +1 и -й элементы, а
- Менябщиеся элементы выделены градиентом
- Теперь изображение соответствует коду, приведенному ниже

Псевдокод Partition¶
Это один из вариантов. Мы можем реализовать рандомизированный вариант или схему Хоара.
- Процесс происходит inplace
- Процесс не гарантирует стабильности
Код:
1 Partition(Array, begin, end): 2 pivot = Array[end-1] // например, мы можем взять элемент из конца 3 i = begin - 1 // да, он может быть < 0, это ОК 4 for j = begin to end-2 // имеется в виду "по элемент end-2 включительно" 5 if Array[j] ≤ pivot 6 i += 1 7 swap(Array, j, i) 8 swap(Array, i+1, end-1) // ставим стержневой элемент на место 9 return i + 1</font>
Список исправлений в псевдокоде:
- Используется
Array[end-1]вместоArray[end] - Используется
swap(Array, i+1, end-1)вместоswap(Array, i+1, end) - Используется
for j = begin to end-2вместоfor j = begin to end-1 - Используется
Quicksort(Array, begin, pivot)вместоQuicksort(Array, begin, pivot-1) - Последнее верно для
QuicksortиTailQuicksort(см. ниже)
</font>
Здесь приведен код, который соответсвует иллюстрации с вебинара, и сама иллюстрация.
Оператор `≤` заменен на `≥`, располагающий меньший и больший массивы соответсвенно справа и слева и "сортирующий" в обратном порядке.
1 Partition(Array, begin, end): 2 pivot = Array[end-1] // например, мы можем взять элемент из конца 3 i = begin - 1 // да, он может быть < 0, это ОК 4 for j = begin to end-2 // имеется в виду "по элемент end-2 включительно" 5 if Array[j] ≥ pivot 6 i += 1 7 swap(Array, j, i) 8 swap(Array, i+1, end-1) // ставим стержневой элемент на место 9 return i + 1</font>

Код на python (с минимальными отличиями от псевдокода)¶
Код показывет разницу между decreasing и increasing partition
def quicksrot(array, begin, end, partition):
if begin < end:
pivot = partition(array, begin, end)
quicksrot(array, begin, pivot, partition)
quicksrot(array, pivot+1, end, partition)
def partition_increasing(array, begin, end):
pivot = array[end-1]
i = begin - 1
for j in range(begin, end-1):
if array[j] <= pivot:
i += 1
swap(array, i, j)
swap(array, i+1, end-1)
return i + 1
def partition_decreasing(array, begin, end):
pivot = array[end-1]
i = begin - 1
for j in range(begin, end-1):
if array[j] >= pivot:
i += 1
swap(array, i, j)
swap(array, i+1, end-1)
return i + 1
def swap(array, i, j):
buff = array[i]
array[i] = array[j]
array[j] = buff
arr = list(range(10))
partition_increasing(arr, 0, 10)
arr
Сортировка в убывающем порядке¶
quicksrot(arr, 0, 10, partition_decreasing)
arr
Сортировка в возрастающем порядке¶
quicksrot(arr, 0, 10, partition_increasing)
arr
Несколько примеров¶
def test(array, partition):
quicksrot(array, 0, len(arr), partition)
assert len(array) > 2
for i, j in zip(array[:-1], array[1:]):
assert i <= j if partition is partition_increasing else i >= j
for i in range(10):
arr = list(range(20))
np.random.shuffle(arr)
cpy = [i for i in arr]
print("unsorted: {}".format(arr))
test(arr, partition_decreasing)
test(cpy, partition_increasing)
print("decreasing: {}".format(arr))
print("increasing: {}".format(cpy))
print("--------------------------")
arr = [1, 1, 1, 1, -4, 5, 5, 5, 5, 56, 5, 5, 5, 5]
cpy = [i for i in arr]
quicksrot(arr, 0, len(arr), partition_increasing)
arr
quicksrot(cpy, 0, len(arr), partition_decreasing)
cpy
Варианты¶
Randomized¶
Если массив организован так, что pivot всегда неудачный - можно обойтись при помощи внесеня рандомизации
Немного вопросов:
Как сделать рандомизацию?
Сколько раз будет генерироваться случайное число?
Какова примерная оценка вероятности того, что всегда будет выбираться наихудший случай? </font>
Hoare Partition¶
Оригинальная схема упорядочения значений, предложенная Хоаром.
Без псевдокода - но его легко найти

wiki/Quicksort - Hoare partition scheme </font>
Хвостовая рекурсия¶
1 TailQuicksort(Array, begin, end): 2 while begin < end: 3 pivot = Partition(Array, begin, end) 4 TailQuicksort(Array, begin, pivot) 5 begin = pivot + 1
Какова будет глубина стека при использовании такого алгоритма?
</font>
Timsort¶
История¶
- Алгоритм изобрел Тим Питерс в 2002 г. для использования в языке Python
- Алгоритм является улучшением merge sort
- ссылка
/* Lots of code for an adaptive, stable, natural mergesort. There are many
- pieces to this algorithm; read listsort.txt for overviews and details. */ </pre> - здесь его даже Timsort не зовут </font>
Особенности алгоритма¶
- Это merge sort на стероидах
- Алгоритм использует неубывающие и невозрастающие последовательности в данных (последние он разворачивает), которые называются run. Ссылки на run'ы отправляются в стек
- Для сортировки маленьких подпоследовательностей < minrun используется insertion sort
- minrun выбирается от 32 до 64 - из соображений, что лучше всего разбивать на части, близкие к степеням двойки
- алгоритм адаптивный, стабильный
- run'ы сливаются по очереди и по ссылкам, что позволяет не выделять большое количество памяти -
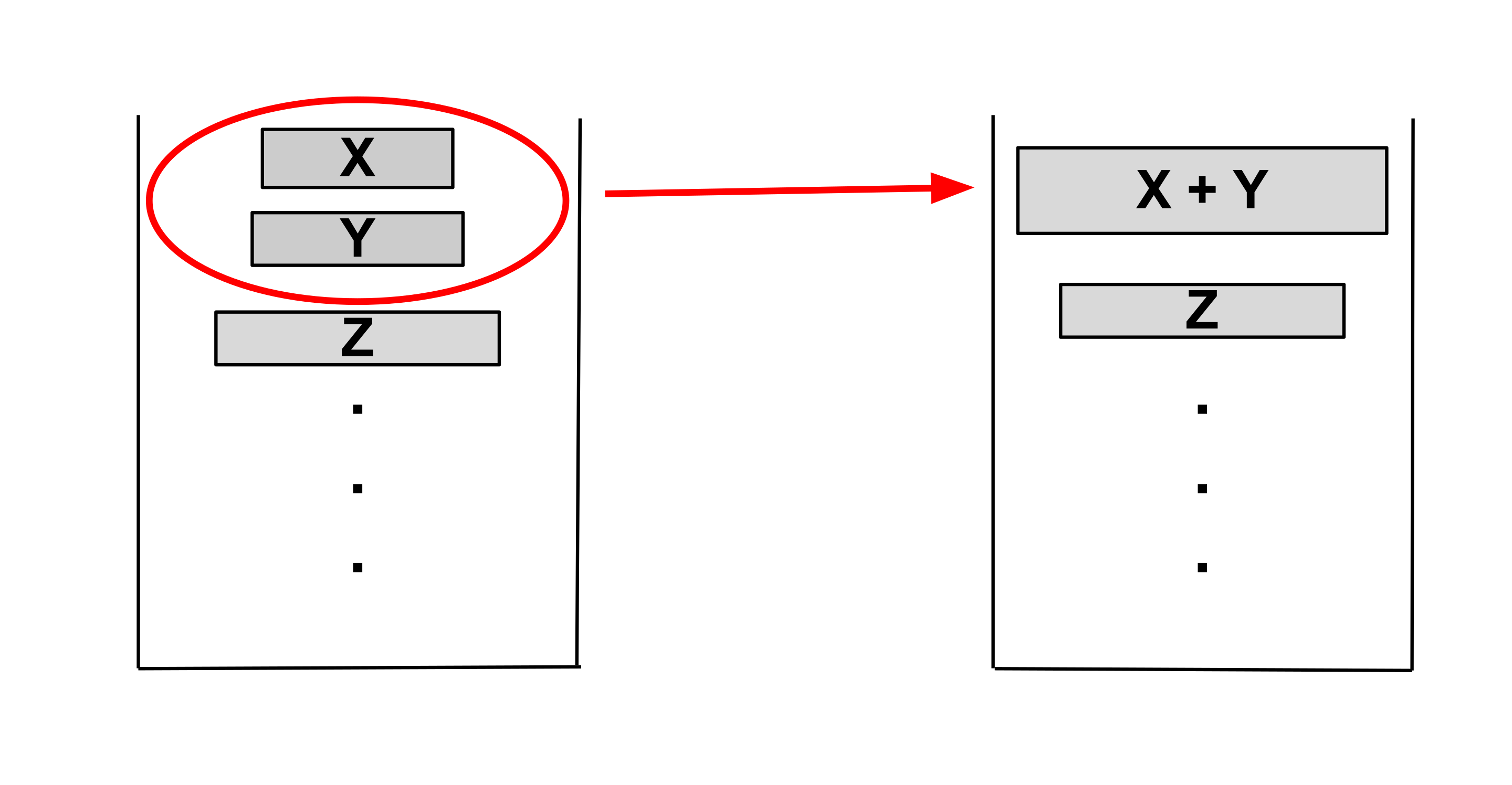
</font>
Ссылки¶
Ссылки на статьи про Timsort на [hackernoon](https://hackernoon.com/timsort-the-fastest-sorting-algorithm-youve-never-heard-of-36b28417f399) и [dev.to](https://dev.to/s_awdesh/timsort-fastest-sorting-algorithm-for-real-world-problems--2jhd)
Домашняя работа¶
Реализовать:
MergeSort или QuickSort (рандомизированный и обычный)
- алгоритм работает корректно, используется insertion sort: 3 балла
- алгоритм работает корректно, но выполняет много лишних действий / отклоняется от реализации не в лучшую сторону - 2 балл
Дополнительно:
- quicksort - сравнить рандомизированный и обычный варианты - 1 балл
mergsesort - добавить обработку run'ов - 1 балл
распараллелить алгоритм - 1 балл (если считаете, что этот материал надо разобрать отдельно - напишите в слак) - 1 балл
делать оба алгоритма не обязательно, но при желании можно, баллы ставятся за лучший :
</font>