Экспоненциальная зависимость

Прошлый урок был посвящён логарифмам. Теперь перейдём к экспоненте.

Экспоненциальная функция — это функция y = eˣ, где e — константа Эйлера, примерно равная 2,7.

С экспонентой удобно работать, потому что её производная — то есть скорость изменения функции в данной точке — равна самой функции.

Экспоненциальная функция обратна логарифму по основанию е.

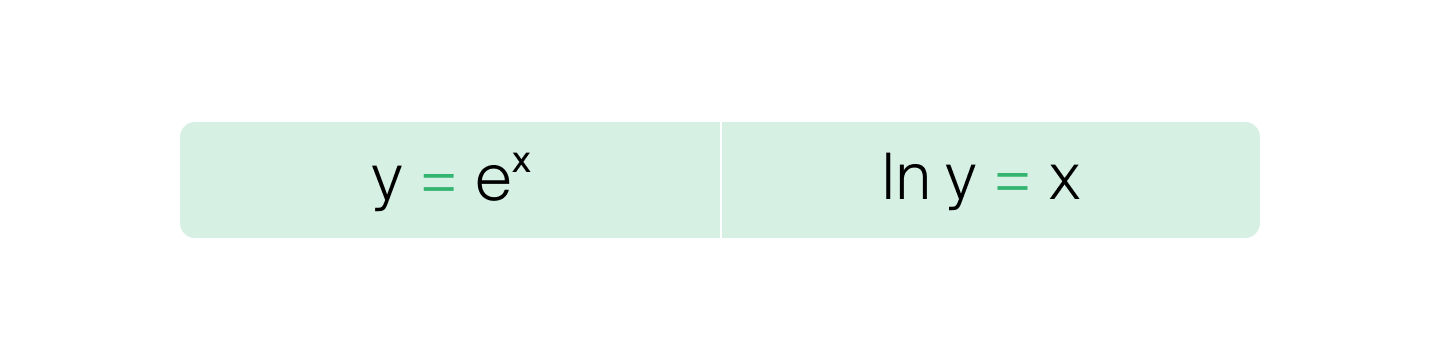
В англоязычной литературе к экспоненциальным функциям также относят показательные. Показательная — это функция f(x) = aˣ, где а называют основанием, x — показателем степени.

Сложность алгоритма считают экспоненциальной, если зависимость сложности от размера входных данных имеет вид экспоненциальной либо показательной функции.

Экспоненциальный рост — возрастание величины, когда скорость роста пропорциональна самой величине. Пример экспоненциального роста — рост числа бактерий в колонии до исчерпания ресурсов. Другой пример — сложные проценты.

У процессов, протекающих экспоненциально, есть общее свойство. За один и тот же промежуток времени их параметры меняются в одинаковое число раз. Банковский вклад каждый год увеличивается на 6%. Снежный ком, катясь с горы, каждую минуту увеличивается в одинаковое число раз.

Иногда логарифмы и экспонента встречаются вместе. Когда играют на фортепиано, частота звуковых колебаний от клавиши к клавише меняется экспоненциально. Но, так как наше восприятие подчиняется логарифмическому закону, кажется, что зависимость линейная.

Рассмотрим графики логарифмической и экспоненциальной функции.

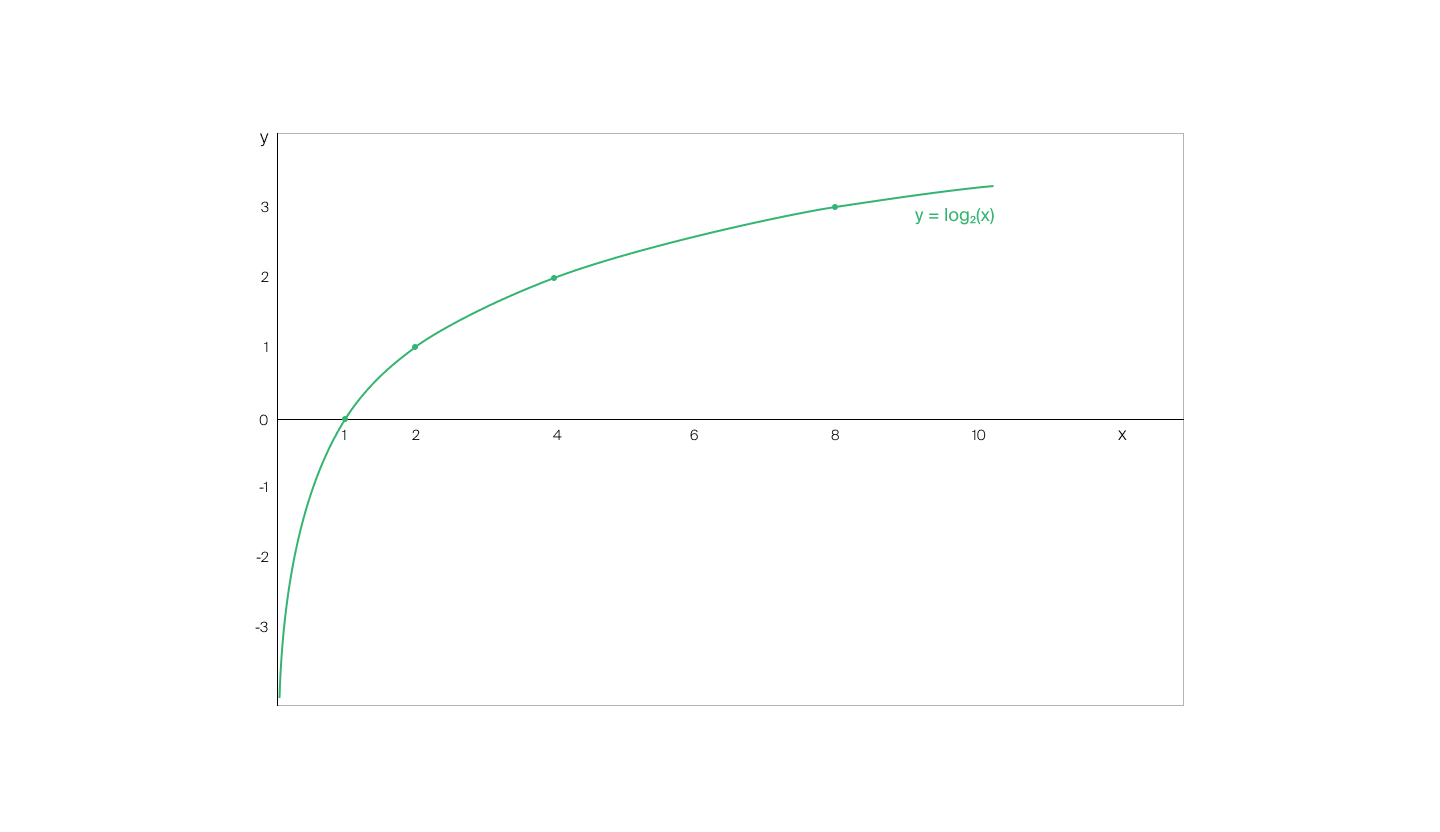
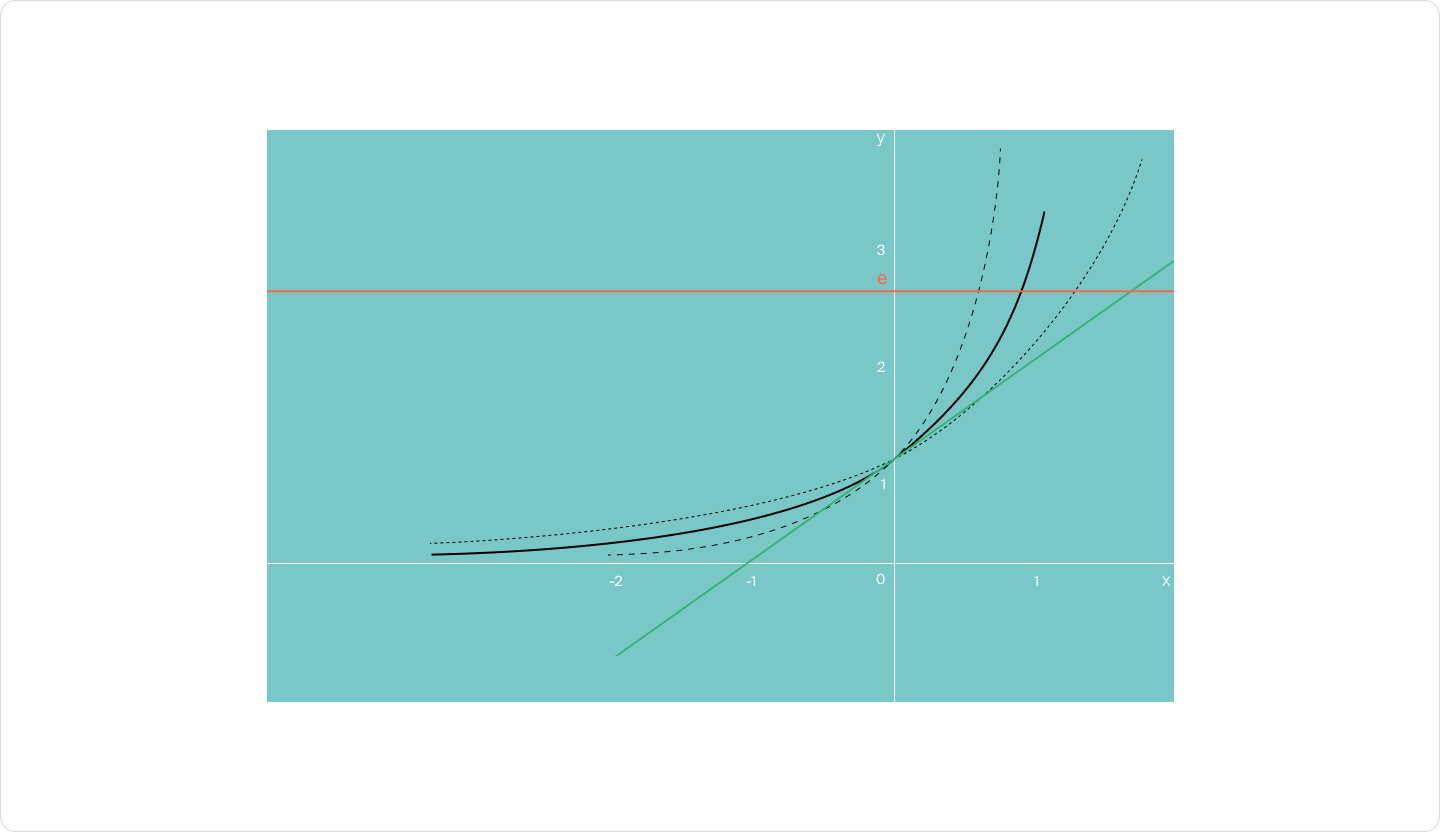
По графику видно, что в случае с логарифмом увеличение значения аргумента влечёт слабый рост значения функции. А для экспоненты значение функции растёт стремительно.

Алгоритмы с экспоненциальной сложностью на практике стараются не применять, так как на больших объёмах данных они требуют слишком много времени.

Представьте, что хакер пытается подобрать пароль к вашему почтовому ящику. Он знает, что в пароле используются только строчные латинские буквы. Длина пароля — n символов. Сколько всего комбинаций хакеру придётся перебрать? Всего их будет $26^n$.

Давайте разберёмся, откуда берётся число $26^n$.

На первом месте может стоять любой из 26 символов и на каждом из семи мест тоже. По теореме умножения вероятностей получим $26^n$. Количество действий в алгоритме экспоненциально зависит от n. Такие алгоритмы работают очень долго. Именно поэтому обычно просят составлять пароли подлиннее. Чем больше n, тем сложнее злоумышленнику подобрать пароль.

Другой пример. Допустим, вы решили заняться трейдингом и пишете алгоритм, который помогает принять решение о покупке или продаже активов. У вас много исторических данных, и для их обработки вы применяете два алгоритма. Один из них имеет логарифмическую, а другой — экспоненциальную скорость роста.

Функция зависимости количества операций от объёма входных данных первого алгоритма имеет вид: y = log₂(x), второго — y равно 2 в степени x.

Допустим, на вход оба алгоритма получают 1000 объектов. В случае логарифмической сложности понадобится десять операций, так как log₂(1000) = 10. Для работы экспоненциального алгоритма понадобится 2 в степени 1000 операций.

Чем больше объектов алгоритм будет получать на вход, тем более существенной будет разница в количестве операций.

На практике большинство алгоритмов имеют дело с большим объёмом данных. Пока второй алгоритм закончит свою работу, ситуация на рынке может поменяться несколько раз. Вряд ли стоит выбирать такой алгоритм для решения реальных задач.

Чтобы чувствовать себя уверенно при работе с логарифмами и экспонентой, выполните задания.